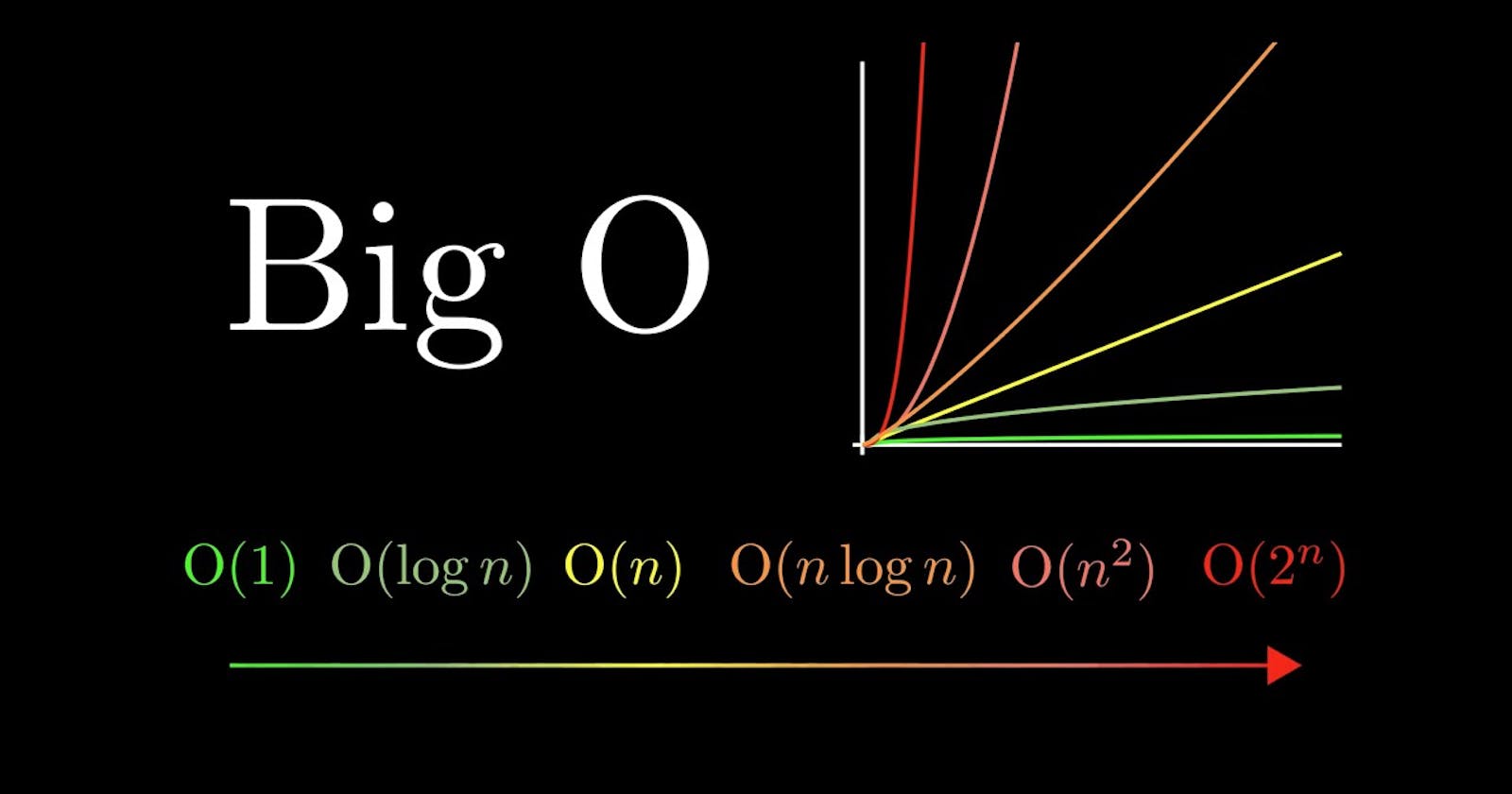Learning Data Structures and Algorithms would inevitably take you through Algorithmic Complexity and Big O notation. I would go on a limb here and say it’s every developer’s goal to write clean code and scalable programs. In order to achieve that milestone, we need to understand Algorithmic Complexity — Big O if you must. I have to set the record straight here, I love things that scale and more so graphical presentation of scales of growth.
What is algorithmic complexity anyway? It’s a measure of how long an algorithm would take to complete given an input size of n. An important note to remember, if a program has to scale, it should compute the result within a finite and practical time-bound even for large values of n.
Because of this reason, complexity is calculated asymptotically as n approaches infinity. In layman’s terms, Big O is a process of calculating the running time of an algorithm in mathematical units to find the program’s limitations, or commonly the “run-time” performance.
An algorithm’s performance according to the rules of Big O analysis is measured in three ways, by determining the best, worst and average case (sometimes known as the Expected case). The concern is with the time required to execute a given task. Big O notation is mostly interested in the worst-case run-time, the O in Big O notation being short for Big Order.
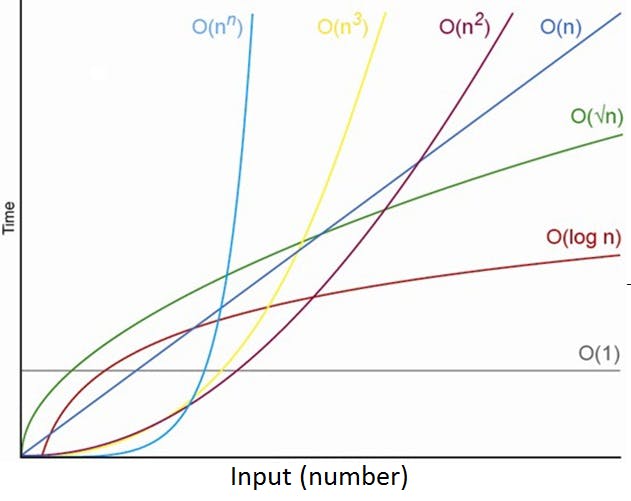
The above graph shows some of the common runtimes and the relation between the input size n and time. To master Big O analysis it is crucial to keep in mind two rules;
- Keep the fastest growing terms
- Drop constants.
Remember, the O in Big O stands for Big Order, so go ahead and drop constants because they are not as significant.
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 12 10:16:23 2022
@author: Andile Jaden Mbele
"""
def get_squared_nums(nums):
squared_nums = []
for n in nums:
squared_nums.append(n * n)
return squared_nums
nums = [2, 4, 8, 9]
get_squared_nums(nums)
# T(n) =>O(n)
If we have statements with basic operations such as comparisons, assignments, reading a variable, etc we assume they take a constant time each ⇒ T(n) ⇒ O(1)
The above code would be Time = a * n + b and after applying some rules we have Time = a * n and we go ahead and drop constants and we’re left with T(n) = O(n)
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 12 10:47:21 2022
@author: Andile Jaden Mbele
"""
def check_duplicates(numbers):
for i in range(len(numbers)):
for j in range(i+1, len(numbers)):
if numbers[i] == numbers[j]:
print(numbers[i], " is a duplicate")
break
numbers = [3, 6, 2, 4, 3, 6, 8, 9]
#T(n) = a * n^2 + b => O(n^2)
The time complexity for the above code is T(n) ⇒ a * n² + b ⇒ O(n²). At this point, I think we can apply some generalizations of our own. The first generalization is that for loop statements result in a runtime of O(n) which is linear, and if we have two of them nested together, our runtime becomes O(n * n) which gives us O(n^2) and that is a quadratic complexity. This is slow, very terrible, and can only be expected from interns.
/*
Created on Tue Apr 12 10:47:21 2022
@author: Andile Jaden Mbele
*/
public class Fib {
void allFib(int n) {
for (int i = 0; i < n; i++) {
System.out.println(i + ": " + fib(i));
}
}
int fib(int n) {
if (n <= 0) {
return 0;
}
else if (n == 1) {
return 1;
}
else {
return fib(n - 1) + fib(n - 2);
}
}
}
It doesn’t seem right to speak of Big O notation and not talk about the Fibonacci series. The Fibonacci code above has two branches per call, and we go as deep as n, therefore the runtime is O(2^n).
Generally speaking, when you see an algorithm with multiple recursive calls, you’re looking at exponential runtime.
Conclusion
To analyse the performance of an algorithm we use Big O notation. Big O provides a high-level understanding of algorithms’ time and space complexity. Overall, the greater benefit of Big O is having clean and optimal code, having higher consistency, resulting in faster apps, ensuring better code readability, efficient refactoring, improved workflow, and more importantly straightforward debugging.
Thank you for reading up to this point. I hope you learned something new. I will also show you some optimal solutions for some of the problems covered here in the future.
Happy Hacking!